The Unsolved Math Problem That Stumps Scientists.

#CollatzConjecture #mathematics #Scientist #ttg #UnsolvedMathProblem

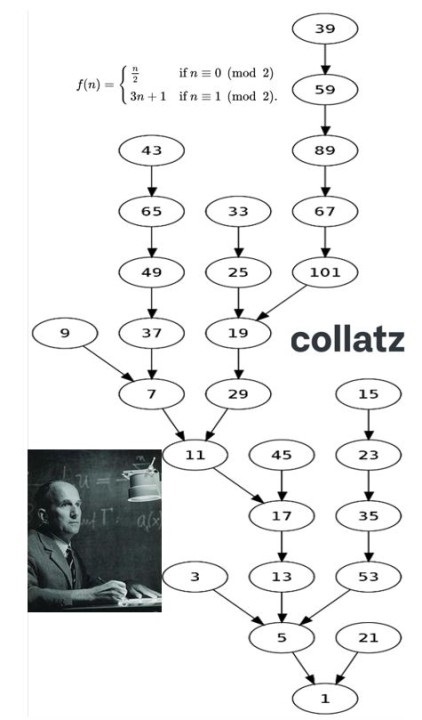
The Collatz Conjecture is a notorious unsolved problem in mathematics that has puzzled scientists for decades. It is a conjecture that states that if you repeat a simple process on any positive integer, you will eventually reach the number 1. This process involves dividing the number by 2 if it’s even or multiplying it by 3 and adding 1 if it’s odd. Despite many efforts, no proof or disproof of the conjecture has been found, and it remains one of the most famous unsolved problems in mathematics. Join us on a journey of discovery as we delve into the mystery of the Collatz Conjecture, a problem that continues to captivate and challenge mathematicians worldwide.

In this article, we take a closer look at the Collatz Conjecture and its implications. We provide examples of the process and a simple Python code implementation. Furthermore, we explore the idea that the solution to this complex math problem may lie in a singularity, just as the ultimate unity of the diverse components of nature comes down to a singular source.

The Collatz Conjecture was first introduced by the German mathematician Lothar Collatz in 1937. He posed the conjecture as a mathematical problem and it has since become a well-known unsolved problem in mathematics. Despite many efforts from mathematicians over the years, proof of the conjecture remains elusive and it continues to be an active area of research.

The Collatz Conjecture starts with any positive integer and follows a simple process: if the number is even, divide it by 2; if it’s odd, multiply it by 3 and add 1. The conjecture states that this process will eventually lead to number 1, but a proof or disproof of this conjecture has not been found.

For example, if we start with the number 3, the steps would be:

1.    Multiply 3 by 3 and add 1, which gives us 10.

2.    Divide 10 by 2, which gives us 5.

3.    Multiply 5 by 3 and add 1, which gives us 16.

4.    Divide 16 by 2, which gives us 8.

5.    Divide 8 by 2, which gives us 4.

6.    Divide 4 by 2, which gives us 2.

7.    Divide 2 by 2, which gives us 1.

Another example, starting with n=97:

1.    Multiply 97 by 3 and add 1, which gives us 288.

2.    Divide 288 by 2, which gives us 144.

3.    Divide 144 by 2, which gives us 72.

4.    Divide 72 by 2, which gives us 36.

5.    Divide 36 by 2, which gives us 18.

6.    Divide 18 by 2, which gives us 9.

7.    Multiply 9 by 3 and add 1, which gives us 28.

8.    Divide 28 by 2, which gives us 14.

9.    Divide 14 by 2, which gives us 7.

10. Multiply 7 by 3 and add 1, which gives us 22.

11. Divide 22 by 2, which gives us 11.

12. Multiply 11 by 3 and add 1, which gives us 34.

13. Divide 34 by 2, which gives us 17.

14. Multiply 17 by 3 and add 1, which gives us 52.

15. Divide 52 by 2, which gives us 26.

16. Divide 26 by 2, which gives us 13.

17. Multiply 13 by 3 and add 1, which gives us 40.

18. Divide 40 by 2, which gives us 20.

19. Divide 20 by 2, which gives us 10.

20. Divide 10 by 2, which gives us 5.

21. Multiply 5 by 3 and add 1, which gives us 16.

22. Divide 16 by 2, which gives us 8.

23. Divide 8 by 2, which gives us 4.

24. Divide 4 by 2, which gives us 2.

25. Divide 2 by 2, which gives us 1.

At this point, n = 1, so the process has stopped and the Collatz Conjecture holds true for this case starting with n = 97.

Simple Python code to implement the Collatz Conjecture:

def Collatz (n): while n != 1:

print(n) if n % 2 == 0:

n = n // 2 else:

n = 3 * n + 1

# Let’s start with n = 97 collatz (97)

Conclusion

Nature is a complex system of both plurality and singularity. On the one hand, it is made up of many different elements and processes that interact with one another to produce the diversity of life we observe. On the other hand, these elements and processes all come from an absolute source – a singular Creator. This Creator gives Nature its ultimate unity, regardless of its diverse components. When we look at Nature as a whole, we see how its plurality ultimately comes down to one singular source. Like all laws of nature, laws of physics and therefore mathematics cannot be contrary to these laws. That’s why the solution to the ‘Collatz Conjecture’ problem is to add a singularity.